E105 - A Simple Climate Model¶
This exercise will not be related to statistics. Instread, you get the chance to write your very own, simple “climate model” that calculates the temporal evolution of the mean temperature of Earth for different simplified, idealised Earths.
Background¶
Preparation for this exercise will only require the close study of the contents of previous lectures. Make sure you are familiar with the concepts of black body radiation, radiative fluxes, Stefan Boltzman Law, heat capacity and dynamic equilibrium.
The essential topics are covered in the Building a Climate III.
Exercise¶
Information¶
Topic |
|
|---|---|
Skills |
|
Creating a Simple Climate Model¶
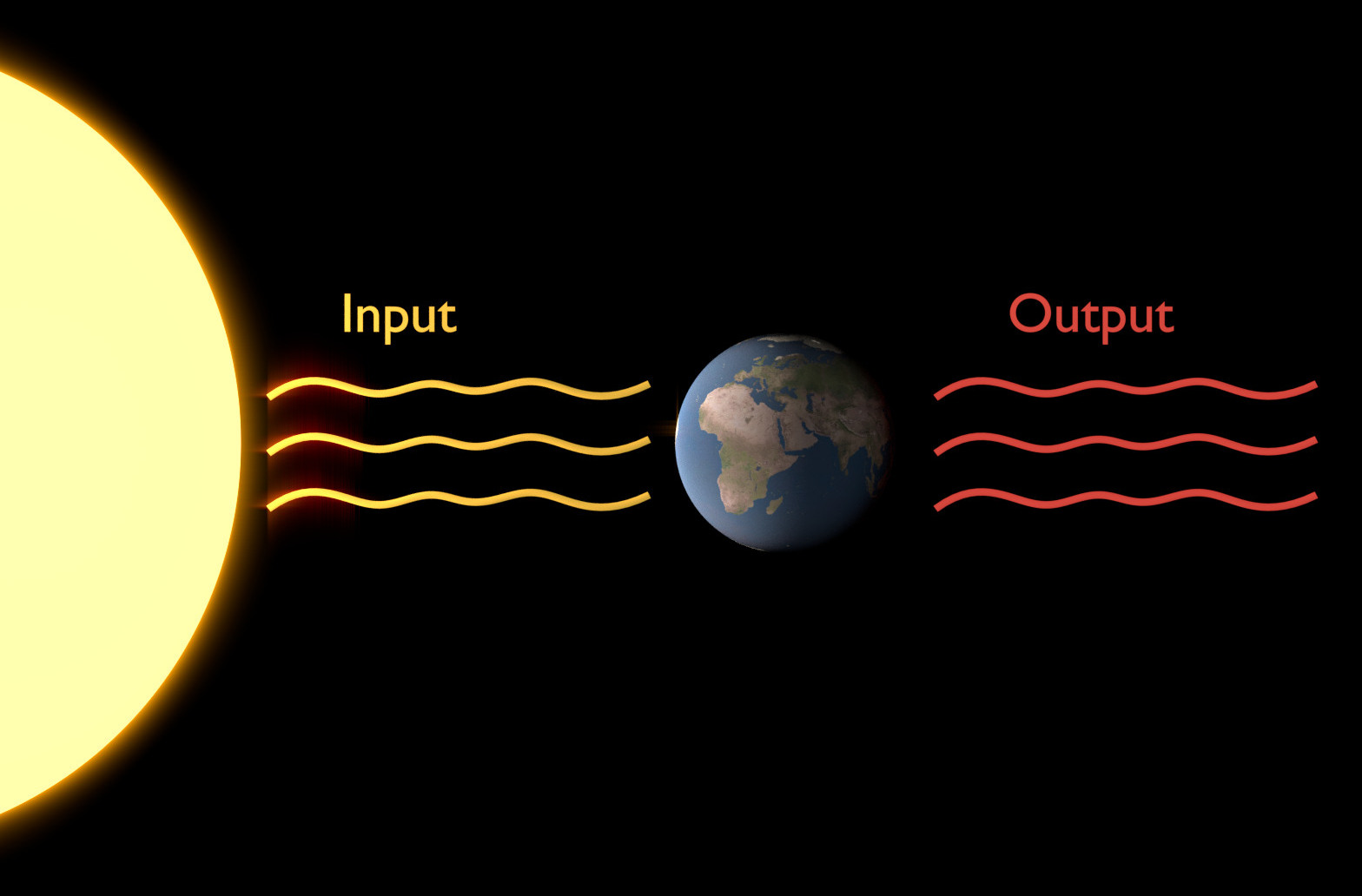
The concept of black body radiation is essential in understanding radiative fluxes (the input and output) of Earth. Specifically, it lets us calculate the nature of incoming and outgoing radiation, as well as the mean global temperatures on Earth or any planet if the whole system is in equilibrium.¶
Study the script below. Certain parameters are already defined for you. Follow the instructions of the script carefully and add your own code where asked. The final script will be able to calculate the temporal evolution of mean global temperatures on different simplified and idealised versions of Earth until an equilibrium is reached.
import numpy
import matplotlib.pyplot as plt
#
"""
Fixed Parameters
================
SB_SIGMA - Stefan-Boltzman constant in W/(m**2 K**4)
PI - delicious old pi
"""
SB_SIGMA = 5.7E-8
PI = 3.141592653589793
"""
Sun's Parameters
----------------
T_SOL - Temperature of the sun (K)
R_SOL - Radius of the sun (m)
"""
T_SOL = 5800
R_SOL = 6.96000E8
"""
Earth's Parameters
------------------
R - distance of Earth from sun (m)
"""
R = 1.5E11
"""
C_AT - heat capacity: atmosphere only
C_OS - heat capacity: ocean surface 50m (real ca. 70m)
C_OU - heat capacity: upper ocean layer 250m (real ca. 360m)
C_OD - heat capacity: ocean 3900m, 70% of Earth surface
Note: Heat capacity is given in J/(K*m^2) to simplify calculations.
The specific heat capacity of air (Cp) is ~1000 J/(kg*K) or, given the density
of air (ro) of 1 kg/m^3, the volumetric heat capacity Cv of ~1000 J/(K*m^3).
[ Cv=Cp*ro=1000 J/(K*m^3) ].
In ro*Cp*dT/dt=dQ/dx, Q is heat flow in W/m^2 or J/(s*m^2), which is given by
f_net. To get dT, we need to divide heat flow by a unit of length. In this exercise,
volumetric heat capacity (c=ro*cp) is already multiplied by 10000 (m), i.e. the
average thickness of the troposphere, and therefore skip the division of the heat
flow by length.
Example:
C_AT= ro*Cp*H where H is the height of the troposphere (~10km).
"""
C_AT = 1.0E7
C_OS = 2.0E8
C_OU = 1.0E9
C_OD = 1.6E10
"""
ALBEDO_0 - albedo mean constant
TRANSM_0 - transmissivity mean constant
"""
ALBEDO_0 = 0.3
TRANSM_0 = 0.64262
"""
Tasks for You!
==============
1) Calculate the sun's output F_SOL and radiative flux PHI_SOL
"""
# your code goes here
"""
2) Calculate F_SW_IN_0, the mean incoming shorwave radiation per area on Earth in W/m^2, i.e. the solar constant.
"""
# your code goes here
"""
3) Calculate the predicted temperature on Earth T_EARTH assuming no atmosphere
"""
# your code goes here
"""
You'll notice that the temperature of task 3 deviates somewhat from the actual temperature on Earth.
What we need is to consider greenhouse gas related transmissivity.
4) Let temperature evolve over time!
Initialise temperature and let it evolve over time until it reaches equilibrium.
Make sure to include albedo and transmissivity in your calculations.
HINT: To calculate temperature change for a specific time step based on net incoming radiation,
remember dT (change in temperature) = dQ (change in heat/energy) / C (heat capacity), incoming
radiation is measured in W/m^2 (J/(s*m^2)) and heat capacity is given in J/(K*m^2) here.
Note: When calculating the radiation emitted by Earth, a multiplication by the factor of 0.95 is
necessary to take into consideration the emissive propertiesof the Earth's surface.
4-a: Initialise temperature at 300K and let it evolve using a heat capacity of the atmosphere only.
4-b: Change the initial temperature, run your code again and see what happens. Does this make sense?
4-c: Pick a different heat capacity and see what happens. Does this make sense?
"""
# your code goes here
Warning
Late submissions won’t be accepted!